
按我写的“换思路再看八卦的数”文中介绍的,将伏羲八卦的阳爻“–”图形看成数字1,将伏羲八卦的阴爻“--”图形看成数字2时,伏羲八卦的各卦图形对应的数为:
本文引用地址:https://www.eepw.com.cn/article/202212/441238.htm乾☰卦为111、兌☱卦为211、离☲卦为121、震☳卦为221、
巽☴卦为122、坎☵卦为212、艮☶卦为122、坤☷卦为222。
这种以1和2字符标识出伏羲八卦的各卦图形的数定义为二的幂进制数。二的幂进制数有3个字符,分别为1、2、0。二的幂进制数的计数规则是满2的值时向上位进1,且进位位恢复系数为1,二的幂进制数转换为十进制数时的方法与二进制数类同,各位的数字符号乘以数位权的和。十进制数转换成二的幂进制数方法比较复杂,可在网上查阅我写的“用整数树的研究成果 探索软件的创新发展” 《软件世界》2008年第8期中介绍的一种转换方法。
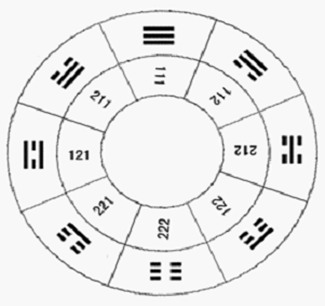
图1:用二的幂进制数标识的伏羲八卦图
一、伏羲八卦树
二的幂进制数是研究伏羲八卦时,按易经中描述的伏羲八卦是“太极生两仪、两仪生四象、四象生八卦、八卦生万物”的二分法生成卦图显示出的规律发现的。
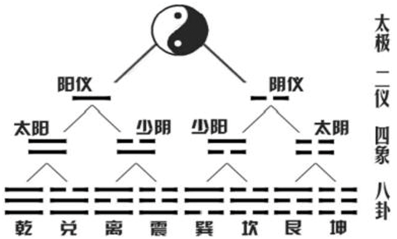
图2:从太极二分法生成伏羲八卦图
将图2太极二分法生成伏羲八卦图中的两仪、四象、八卦中的阳爻“–”图形看成数字1,阴爻“- -” 图形看成数字2替代后,可得到图3。
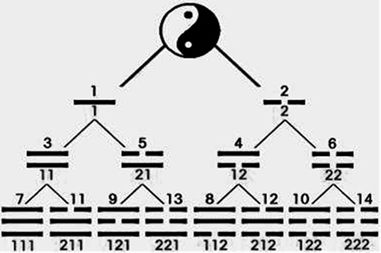
图3:用二的幂进制数和十进制数标识的太极生成伏羲八卦图
在图3用二的幂进制数和十进制数标识的太极生成伏羲八卦图中,两仪、四象、八卦的下面标注的是对应的二的幂进制数,上面标注的是对应的十进制数。再将图中两仪、四象、八卦的各卦位置看成一个个结点时,伏羲八卦就是一个二叉树。
在数据结构研究中,人们为了快速检索数据,设定了二叉树、B+树、基数树等许多种二叉或多叉树,统称为检索树。检索树的生长过程是:在根结点下有1个以上子结点,构成第一层子结点。按设定需要,第一层的各子结点做为父结点还可有1个以上子结点,构成第二层子结点……,如此,可生长出若干层子结点,构成某种检索树。各种检索树的每层结点的个数、生长的方式和标识等都有所不同。
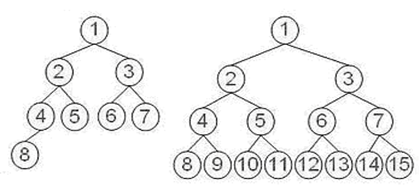
图4:二叉检索树图 右侧为完全二叉检索树
将图3伏羲八卦的二叉树中的太极看做二叉树的第一层父结点,则与数据结构中的完全二叉检索树的图形结构完全一样,如同图4中的右侧的完全二叉检索树,也都有15个结点,也都可用于数据检索,但是这两个二叉树的特征有很大不同。
二、伏羲八卦是二叉整数树
根据伏羲八卦生万物的认识,按照二分法生成规律,八卦可无限层往下分出卦。将图3太极生八卦图中太极看成0层,两仪看成1层,四象看成2层,再二分可得到3层即为八卦层。将每层的各结点用十进制数(不是完全二叉树的结点顺序号)表示该结点对应的二的幂进制数值后,可得到图5四层二叉树。(再下分2层,就是64卦,在此不多述)
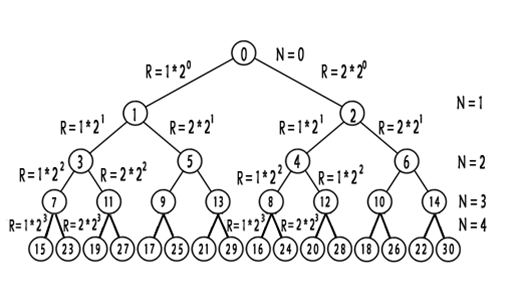
图5:伏羲八卦二叉树前0至4层结点分布图
在图5伏羲八卦二叉树前0至4层结点分布图中0至30十进制整数一个不缺,一个不重复地有规律排列着。已证明,伏羲八卦二叉树再二分下去至N层(N为无限大正整数)时,也都有对应的整数按规律分布在各层的结点上。
整数有无限多是天量,伏羲八卦二叉树也有无限多天量结点可使无限多天量整数有规律地排列在对应结点上。因此将伏羲八卦二叉树称为整数二叉树。正如整数有负整数一样,二叉整数树也还有以0为父结点的镜像的负整数二叉树,在此不多述。
研究整数二叉树发现整数树上的各结点的一些排列规律:
1、所有整数中的奇数都排列在根结点0的第一子结点1及它下面的分叉树的各层结点上。所有整数中的偶数都排列在根结点0的第二子结点2及它下面的分叉树的各层结点上。
2、整数二叉树上所有父结点与其第一子结点的差值R=1*2n(n为父结点的层数),与其第二子结点的差值R=2*2n。
3、整数二叉树上所有父结点的第一子结点与第二子结点的差值R=1*2n(n为父结点的层数),等等。
整数除了以二叉树存在,还以1为差的整数一叉树即等差数列存在,还以3至m(m为无限大正整数)叉树存在。下图是整数4叉树:

图6:整数4叉树图
在数据结构中介绍有多种和多叉检索树。
所有检索树的共同特点是:
1、树结构是人为设置
2、各层结点个数不固定
3、各结点上的数据不固定
4、树的层(深度)是有限的
研究发现,所有整数树的共同特点是:
1、树结构不是人为设置,是客观存在
2、各层结点个数固定和完整
3、各结点上的数据是1个固定不变的整数
4、树的层(深度)是无限的
简单说,整数树是客观存在的,检索树是人为设定的。
三、天量数据与检索算法
信息技术是用计算机对数据处理的技术。计算机数据处理操作主要分三步:数据输入、数据计算、数据输出。通常计算机的运算速度是决定数据处理速度的主要因素。但是随着需要处理的信息量和信息源种类的增多,如何快速地相应提高数据输入和数据输出的速度也成为重要因素。在许多不匹配的信息处理中,常常计算机在等待计算数据的提供,在浪费计算资源。影响数据的输入和输出时间的原因是计算机的外部设备寻找数据的存取时间慢。有诸多因素造成数据的存取时间慢,其中查找数据存取地址的检索算法优劣是最主要因素,尤其在需处理的数据量非常大时。
人们已习惯将非常大的数据量称为海量数据,是可以理解的。但是,常有一些公司将他们的产品的处理数量宣传为海量就不科学了。因为称为海的大小不一,如中南海、北海、东海等等都是不同大的。
在自然界中海是有边界的,海量也是是有限量,只有天无边界,可称为天量。目前没有一家公司产品能狗快速处理天量数据。因为在迄今为止的数据结构中的队、栈、表、图、树等等数据检索的方法都是在有边界的闭区间内的检索的方法,即对有起始数据A和终止数据B之间的检索;不能在开区间,即对有起始数据A,没有终止数据B的无限增长的数据检索,因为没有发现和发明对应的数据结构。
世上有无限增长的量吗?有!我们天天用的数就是无限增长的量,例如整数就是无限增长的天量,并且所有数都源自整数。那有需要处理天量数据的应用需求吗?有!在智慧城市中的千千万万个摄像头在不断产生的视频信息就实天量,需要快速检索处理。在信息化快速发展的时代,凡无边界在增长的数据都有必要按天量数据进行设置和处理。否则,如按闭区间的检索设置和处理,今后可能会有重新要设置的麻烦问题。
那有快速处理天量数据的检索算法吗?有!就是源自伏羲八卦二叉整数树的数据结构启发的检索方法。
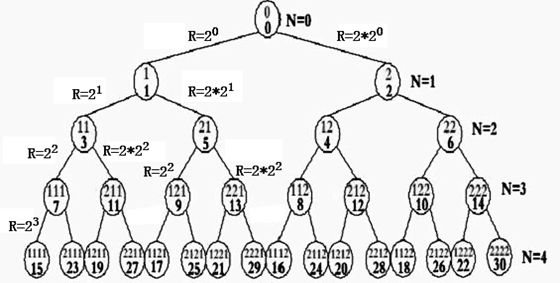
图7:伏羲八卦整数树的前0至4层数据结构图
图7是在前面伏羲八卦二叉树前0至4层结点分布图上在每个结点内增加了对应该结点的二的幂进制数显示,标识的这些二的幂进制数的值与该结点标识的十进制数的值相等。
检索技术的核心是如何快速查找出数据存取地址,为此人们研究出队、栈、表、图、树等数据结构和哈希算法等多种算法。伏羲八卦整数树能对天量数据快速检索是基于发现了它的独特的数据结构和在该数据结构上研究出的检索算法。
对照图7伏羲八卦整数树的前0至4层数据结构图,伏羲八卦整数树有一些利于能对天量数据快速检索算法的特征。归纳有:
1、伏羲八卦整数树对应天量整数有可无限增长的天量结点。
此点已做说明,不再多述。
2、伏羲八卦整数树的层数为N(N为0至无限大正整数)。从N=1层开始,每N层位置码的位数等于层数N。
例如:N=2层(四象层)的对应四象的4个二的幂进制数都是2位。N=3层(八卦层)的对应八卦的8个二的幂进制数都是3位。
3、伏羲八卦整数树的各结点的二的幂进制数是从0根结点二分法产生。将各结点的二的幂进制数定义为该结点的位置码后,可看到每个第1子结点的位置码(二的幂进制数)是在其父结点的位置码前(左侧)添数字1产生。每个第2子结点的位置码是在其父结点的位置码前(左侧)添数字2产生。
例如:N=2层(四象层)的对应的4个结点中,第1和第2结点的位置码是在它们的父结点1的位置码前分别添上1和2产生(左分叉添1,右分叉添2),即为11、21。第3和第4结点的位置码同样是在它们的父结点2的位置码前分别添上1和2(左分叉添1,右分叉添2)产生,即为12、22。
4、伏羲八卦整数树的结点是二分发产生的,每个结点的位置码都据有遗传基因,可向上查到该结点的父结点至根结点位置码,也可下推算出该结点的两个子结点位置码和这两个子结点的所有无限多的的各层子结点的位置码。
例如;在伏羲八卦整数树的前0至4层数据结构图中选N=3层中间结点数为8的结点,该结点的位置码是112。从这个结点的位置码112可看出后两位12是该结点的父结点的12的位置码。还可看到这个结点的位置码112的最后位2是该结点的父结点的12的父结点2的位置码。
在这个该结点数为8的结点位置码112上按照伏羲八卦整数树的子结点位置码二分发产生规则,首先在该结点位置码112前(左侧)添上1产生该结点的第一子结点位置码1112。再在该结点位置码112前(左侧)添上2产生该结点的第二子结点位置码2112。用同样的规则还可很容易下推算出这两个子结点的所有无限多的的各层子结点的位置码。
5、因的各结点的位置码就是该结点的二的幂进制数,也就是各结点的位置码的值等于该结点十进制整数值。这是伏羲八卦整数树数据结构优于所有人为设计的数据结构的特性。伏羲八卦整数树可检索天量数据,且数据存取地址数不用查找和计算,直接等于唯一对应整数。
在伏羲八卦整数树仅发现的这5种数据结构特性,就可得到多种对天量数据快速检索的算法。
简单举例:将某一需存取的数据,如不是整数,转换为整数后假设为十进制数24,再将24转换为对应的为2112,也就是在伏羲八卦整数树上的存取位置码,按该位置码可有以下查找算法供参考:(请参照图7)
算法1:因十进制数24的二的幂进制数为2112是4位数,按在伏羲八卦整数树的存取结点的二的幂进制数与该结点位置码相同,且位数等于层数N的特性,直接在N=4层结点中顺序查找或设计一个算法查找。在本例中,十进制数24的存取位置可快速查出在N=4层的第10个结点。
算法2:根据伏羲八卦整数树的各结点对应的二的幂进制数(位置码)据有遗传基因特性,在已知十进制数24的二的幂进制数(位置码)为2112时,将24的二的幂进制数(位置码)2112最右侧位值2为一个位置码,在伏羲八卦整数树的N=1层查到对应结点2为起始结点,再依据24的二的幂进制数(位置码)2112右侧第二位是1向左下侧查到12结点,然后再依据24的二的幂进制数(位置码)2112右侧第二位是1向左下侧查到112结点,最后再依据24的二的幂进制数(位置码)2112右侧第3三位是2向右下侧查到2112结点,用4步就查到十进制数24的存取位置2112结点。
以上介绍的是利用伏羲八卦整数树快速检索天量数据的原理和简单检索算法,希望能给大家一个启发。感兴趣的人士可在网上查阅我写的“整数树结构与天量数据快速检索”一文,做更多的了解,在进行更深入的研究后,发明出更新的信息技术。
